
This of course assumes "blind" stacking, whereas many possibilities would be aborted after 2 or 3 cubes if one was paying attention. Due to loops and various symmetries that create multiple solutions the probability is closer to 1/1000. Then for large instance sizes (say N = 100) the branching would overwhelm the computer's memory.įor a sophisticated depth-first routine to find (all) solutions quickly of puzzles up to size 100, please Google: Chris Reeser.įinally in Tutte's 1947 paper he says that the chances of hitting on the solution of the particular puzzle he uses as an example is less than one in 40,000.

But supposing someone was utilizing a breadth-first search and the puzzle was a stack of monochromatic cubes so that every arrangement led to a solution.

One is tempted to say that puzzles with no solution are harder to determine than ones with solutions. Obviously this particular instance was constructed so that there is no immediate way to determine the answer, namely, no solution. There are 4 quick choices to continue this thread to cubes 3 and 4 none of them complete a half solution. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more.
No solution graph free#
Choosing 2: g-r also leads, after a couple steps, to a dead end. Explore math with our beautiful, free online graphing calculator. Now choosing 2: r-y leaves nothing available for 3. Thus, the pair 1: r-y MUST be used in any solution. But it is impossible to complete this thread with what is available left on cubes 3 and 4. Now if a complementary thread takes 1: G-R then a short check shows 2: R-Y is impossible, leaving 2: B-G. Use distributive property on the right side first. Free graphing calculator instantly graphs your math problems. And 4: Y-G, leaving no possible choice for cube 3. If the coefficients are the same on both sides then the sides will not equal, therefore no solutions will occur. Now if a complementary thread has 1: R-Y then it must have 2: B-G. Therefore if a complete thread exists in this case we must have 2: g-r. Then it is easy to rule out 2:b-g (no choice for 4), 2: r-y (no choices for 3 and 4). Suppose one half solution (complete thread) takes 1: b-g. (Had there been a solution then there would be no obstacle and we would have an existence proof for solvable.) Of course we are assuming we don't have access to a look-up table of all possible obstacles or "blocks" that can occur for puzzles of this size, otherwise we would quickly find a block. The instance is easier as N = 4, small size, but relatively harder as each color shows up six times. A) no solution B) x 3 C) x 3 D) Subjects English History Mathematics Biology Spanish. In the two previous examples we have used the word “free” to describe certain variables.Just like determining lower bounds is generally harder than "finding" upper bounds, so proving no solution for this puzzle is not immediate. Use the graph of the function f to solve the inequality.
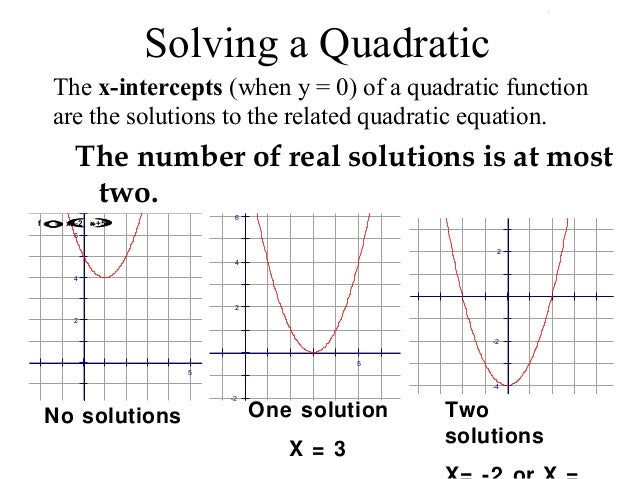
(By the way, since infinite solutions exist, this system of equations is consistent.) Try plugging these values back into the original equations to verify that these indeed are solutions. Look at the slope and y-intercept solve both equations for y to get slope-intercept form, y mx + b.

Since we have infinite choices for the value of \(x_3\), we have infinite solutions.Īs examples, \(x_1 = 2\), \(x_2 = 3\), \(x_3 = 0\) is one solution \(x_1 = -2\), \(x_2 = 5\), \(x_3 = 2\) is another solution. Look at the graph if the two lines are parallel (they never touch), then there is no solution to the system. Example 2: Determine whether the following system of equations have no solution, infinitely many solution or unique solutions. Hence the system of equations has no solution. So they intersect each other at an infinite number of points. Once \(x_3\) is chosen, we have a solution. Without graphing them, we can see that both have the same slope -3 which means lines are parallel. The simple reason is the 2 equations represent 2 lines that overlap each other. As we saw before, there is no restriction on what \(x_3\) must be it is “free” to take on the value of any real number. These two equations tell us that the values of \(x_1\) and \(x_2\) depend on what \(x_3\) is.


 0 kommentar(er)
0 kommentar(er)
